Undergrad math wiz publishes theory about Fibonacci numbers

January 10, 2020June 30, 2022last updated on June 30, 2022 at 15:33 Featured Science & Mathematics Students

In mathematics, a Fibonacci Sequence is a string of numbers where each number is the sum of the two numbers that come before it.

A Fibonacci Sequence starts with 1, 1, 2, 3, 5, 8, 13, 21, 34 — and it goes on and on after that.

Much in the same way a Fibonacci Sequence builds on what came before — Citadel cadet Matthew Blair took what his professors taught him and turned it into an academic paper on the mathematical sequence.

Antara Mukherjee, Ph.D., Cadet Matthew Blair and Rigoberto Flórez, Ph.D.

Blair, along with co-authors Rigoberto Flórez, Ph.D., and Antara Mukherjee, Ph.D., wrote an academic paper titled “Matrices in the Hosoya Triangle.” The article was published in The Fibonacci Quarterly, the primary publication of The Fibonacci Association since 1963.

Most authors who are published in academic journals are professionals who already work in their areas of expertise; it’s unusual for a student to be published alongside those established professionals.

The focus of Blair’s research is on a Hosoya Triangle, which is when Fibonacci numbers are arranged in a triangle, rather than a straight line.

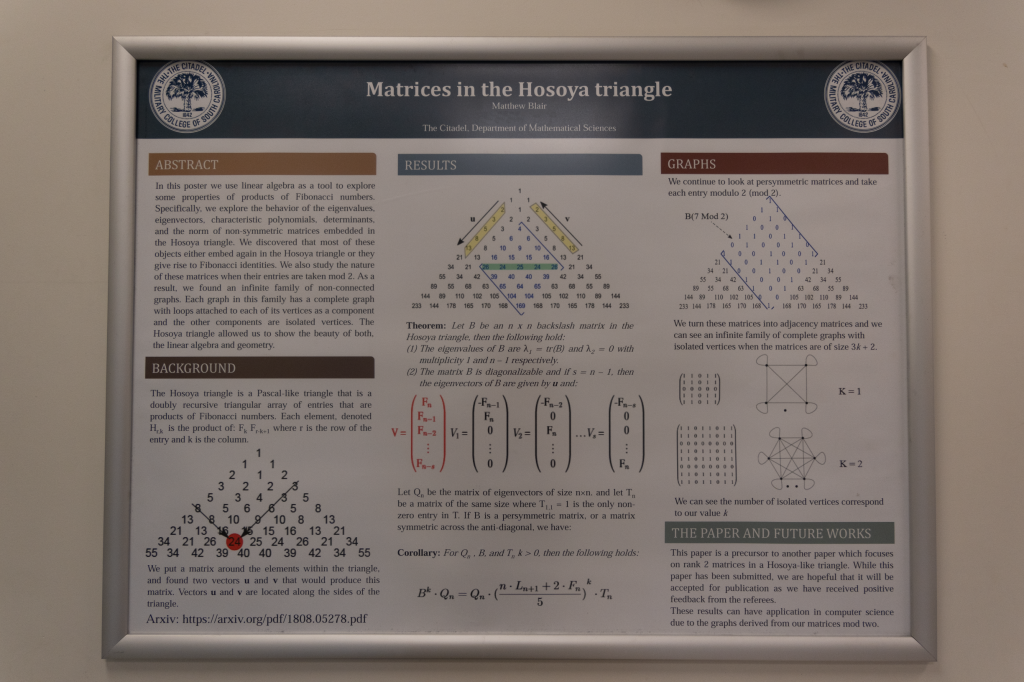
“We used linear algebra on a triangular array whose entries are products of Fibonacci numbers,” said Blair. “By encapsulating these entries in a matrix, we found several unique properties that highlight the beauty of the geometry.”

In this paper, we use well-known results from linear algebra as tools to explore some properties of products of Fibonacci numbers. Specifically, we explore the behavior of the eigenvalues, eigenvectors, characteristic polynomials, determinants, and the norm of non-symmetric matrices embedded within the Hosoya triangle. We discovered that most of these objects either embed themselves within the Hosoya triangle, or they give rise to Fibonacci identities.
From Cadet Matthew Blair’s paper abstract statement

The entire academic paper can be found here.

Blair is a senior Computer Science major from Anderson, South Carolina. He has also presented his work at several conferences including Kennesaw State University Mathematics Conference, the Mathematical Association of America and the INTEGERS Conference.